[2012 Siggraph] Background: Physics and Math of Shading

Background: Physics and Math of Shading 

Naty Hoffman

Slide PDF <https://blog.selfshadow.com/publications/s2012-shading-course/hoffman/s2012_pbs_physics_math_slides.pdf>

Course note <https://blog.selfshadow.com/publications/s2012-shading-course/hoffman/s2012_pbs_physics_math_notes.pdf>

 

번역: Doov with Google Translate

빛이 물질과 상호 작용할 때 일어나는 일의 물리학부터 시작하겠습니다.

We’ll start with the physics of what happens when light interacts with matter.

 

 

Light and Media

균일한 매질(Medium)을 통한 빛

가장 단순한 경우는 균일한 매질을 통해 빛이 번지거나 모든 곳에서 동일합니다. 이 경우 빛은 직선으로 움직입니다.

The simplest case is light propagating through a homogeneous medium, or one that is the same everywhere. In this case light moves in a straight line.

 

 

투명한 매체

일부 균일한 매체 (깨끗한 물 또는 유리와 같은)는 가시광선에서 간신히 빛을 흡수합니다.

Some homogeneous media (like clean water or glass) barely absorb light in the visible spectrum.

 

 

맑은 흡수성 매체

다른 균일한 매체는 눈에 보이는 스펙트럼의 빛을 눈에 띄게 흡수합니다. 위와 경우에는 빨간색보다 푸른빛이 더 많이 흡수됩니다.

Other homogeneous media noticeably absorb light in the visible spectrum - in this case more blue light than red is absorbed.

 

 

규모

규모(Scale)는 중요합니다. 예를 들어, 물은 가시 광선 스펙트럼의 적색 부분에서 약간의 빛을 흡수하지만 몇인치 이상 눈에 띄지는 않습니다.

Scale is important. For example, water does absorb a little light in the red end of the visible spectrum, but it’s not noticeable over a few inches.

 

 

그러나 이 흡수는 수십 야드 거리에서 상당히 중요합니다.

But this absorption is quite significant over distances of dozens of yards.

 

 

매체(Medium)가 균일하지 않은 경우에는 어떻게 합니까?

이는 굴절률 (빛에 영향을 주는 물질의 특성)이 변한다는 것을 의미합니다. 

빛은 여전히 직선으로 움직일까요?

That means the index of refraction (the property of matter that affects light) changes. Will it still move in a straight line?

 

 

산란

굴절률의 급격한 변화는 산란을 일으켜 광전파의 방향을 바꿉니다.

빛의 양은 동일하게 유지됩니다 (양과는 다르지만 방향을 바꾸는 흡수와는 다릅니다)

Abrupt changes in the index of refraction cause scattering, which changes the direction of light propagation; amount of light stays the same (unlike absorption, which changes amount but not direction)

 

 

빛과 물질의 상호작용

• 흡수: 강도 / 색 변화, 방향 변화 없음
• 산란: 방향 변화, 강도 & 색 변화 없음
• 방출(새로운 빛 창조, 대부분의 머터리얼과 관련이 없음)

요약하면, 우리는 빛 / 물질 상호 작용의 세 가지 기본 모드를 갖습니다 : 흡수, 산란, 방출 (마지막-방출은 더 이상 논의되지 않을 것).

To summarize, we have three basic modes of light / matter interaction: absorption, scattering, and emission (the last one will not be discussed further)

 

 

흐린 매체

흐린 매체는 빛의 방향을 다소 무작위화 시키기에 충분한 산란을 일으킵니다.

Cloudy media cause enough scattering to somewhat randomize the light direction. 

 

 

과도한 산란의 규모 문제

흡수(absorption)와 마찬가지로, 산란에 대한 스케일도 중요합니다. 

공기는 수 야드 이상으로 눈에 띄게 퍼지지 않지만 마일을 넘어섭니다.

Like absorption, scale matters for scattering: air doesn’t scatter noticeably over a few yards, but it does over a scale of miles.

 

 

불투명 또는 투명한 매체

불투명 (또는 반투명) 매체는 빛의 방향을 완전히 무작위화 시키기에 충분한 산란을 일으킵니다.

Opaque (or translucent) media cause enough scattering to completely randomize the light direction.

 

 

흡수과 산란

균일한 매질의 외관은 흡수 및 산란 특성의 조합에 의해 결정됩니다.

The appearance of a homogeneous medium is determined by the combination of its absorption and scattering properties.

 

 

수평면에서의 산란: 반사 & 굴절

• 이 특수한 산란은 반사와 굴절의 두 방향으로 빛을 나눕니다.
• 굴절된 빛이 흡수되어, 표면 아래에서 산란됩니다.

중요한 산란 특수 케이스 : 두 개의 굴절률 사이의 완벽히 평평한 (광파의 크기까지) 평면. 

임의의 수의 산란 방향으로 분할하는 대신 (일반적인 경우에서처럼),이 경우 빛은 반사와 굴절의 두 가지 방향으로 정확히 분리됩니다.

Important scattering special case: a perfectly flat (up to the size of light waves) plane between two indices of refraction. Instead of splitting up into an arbitrary number of scattering directions (as would happen in the general case), in this case light splits into exactly two directions: reflection and refraction.

 

 

비광학 평면: 마이크로 지오메트

• 각 표면의 점은 한 방향으로 빛을 반사합니다.
• 표면 모양은 표면 방향이 다른 많은 점들의 집합 결과입니다.

광파장의 크기까지의 표면 (예를 들어, 하이 엔드 망원경 광학)은 광학적으로 평면이다 - 그러나 대부분의 표면은 빛의 반사에 영향을 미치는 마이크로 지오메트리 (광파장보다 크지만 픽셀보다 작은 범프)을 갖는다.

A surface which is flat up to the size of light wavelengths (e.g. high-end telescope optics) is optically flat - however, most surfaces have microgeometry (bumps bigger than a light wavelength but smaller than a pixel) that affect light reflection.

 

 

거칠거칠한 = 뭉개진 반사

이 두 표면은 육안으로 똑같이 매끄럽게 보입니다. 그러나 현미경에서 우리는 거칠기의 차이를 볼 수 있습니다. 상단의 표면은 약간 울퉁불퉁합니다. 들어오는 광선은 약간 다른 각도의 표면 비트를 쳐서 약간 다른 출사 방향으로 반사됩니다. 바닥에 있는 표면은 현미경 스케일에서 매우 튼튼합니다. - 들어오는 각 광선은 매우 다른 방향으로 향하는 표면 조각을 때리며, 나가는 광선을 넓은 방향의 원뿔 위에 펼칩니다. 두 물체의 반사의 차이점에서 결과를 볼 수 있습니다.

Both of these surfaces look equally smooth to the naked eye; however under a microscope we can see the difference in roughness. The surface on the top is only slightly bumpy; the incoming light rays hit bits of the surface that are angles slightly differently and get reflected to slightly different outgoing directions. The surface on the bottom is very rugged on the microscopic scale - each incoming light ray hits a piece of surface that is oriented very differently, spreading the outgoing light rays over a wide cone of directions. We can see the results in the differences between the reflections off the two objects.

 

 

거시적인 관점

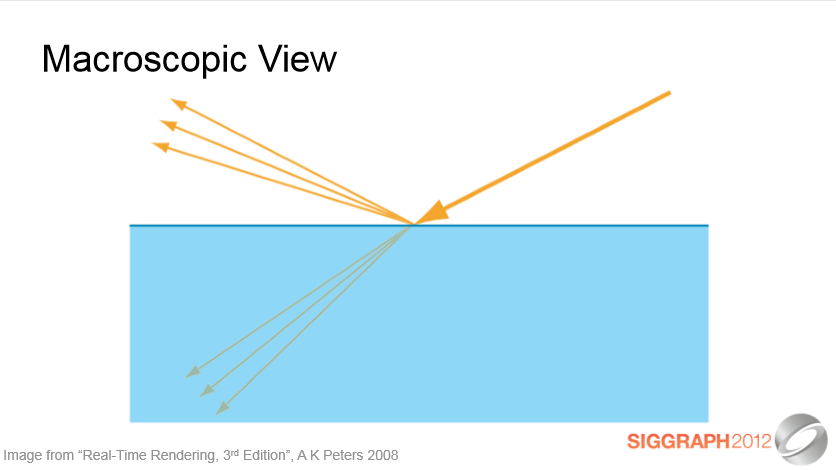
거시적 관점에서, 우리는 마이크로 지오메트리를 통계적으로 취급하고 표면을 여러 방향으로 반사 (그리고 굴절)하는 것으로 봅니다.

In the macroscopic view, we treat the microgeometry statistically and view the surface as reflecting (and refracting) light in multiple directions

 

 

굴절된 빛은 어떻게 될까요? 

물체가 어떤 종류의 재료로 만들어 졌는지에 달렸습니다.

What happens to the refracted light? It depends what kind of material the object is made of.

 

 

금속

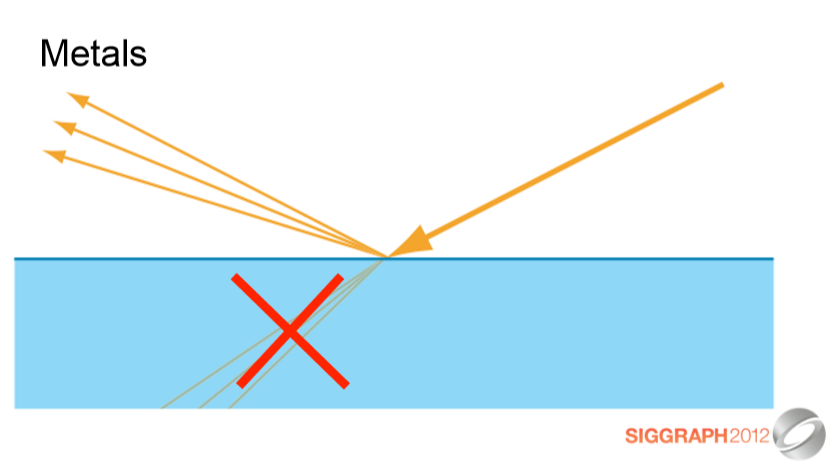
금속은 즉시 모든 굴절된 빛을 흡수합니다.

Metals immediately absorb all refracted light.

 

비금속(절연체, 유전체)

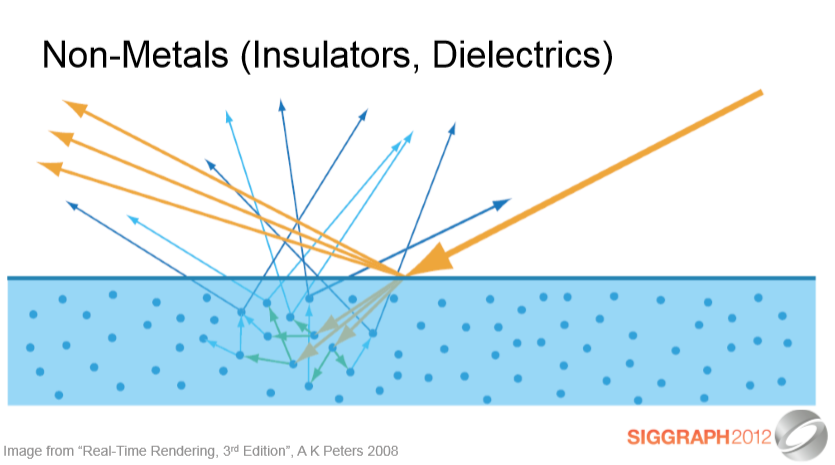
비금속은 이전에 본 액체 잔처럼 행동합니다. 그들은 다양한 정도의 흡수와 산란을 일으킨다.

굴절된 빛은 물질 내부에서 흩어지고 흡수되며 일부는 다시 나옵니다.

Non-metals behave like those cups of liquid we saw earlier. They cause various degrees of absorption and scattering; 

the refracted light gets scattered and absorbed inside the material and some of it comes back out.

 

 

규모 그리고 표면하산란

재방출된 빛은 진입점으로부터 다양한 거리에서 나옵니다. 거리의 분포는 산란 입자의 밀도 및 특성에 의존합니다.

The re-emitted light comes out at varying distances from the entry point. 

The distribution of distances depends on the density and properties of the scattering particles.

 

 

규모 그리고 표면하산란

출입구 거리에 비해 픽셀 크기 (또는 샘플 사이의 거리)가 클 경우 (녹색 원), 거리가 효과적으로 0이라고 가정할 수 있습니다.

If the pixel size (or distance between samples) is large (green circle) compared to the entry-exit distances, we can assume the distances are effectively zero.

 

 

규모 그리고 표면하산란

출입구(Entry-to-exit) 거리를 무시함으로써 우리는 모든 쉐이딩을 한 지점에서 로컬적으로 계산할 수 있습니다. 

음영 처리 된 색상은 표면의 한 점에 부딪힌 빛의 영향을 받습니다.

By ignoring the entry-to-exit distance, we can then compute all shading locally at a single point. 

The shaded color is only affected by light hitting that surface point.

 

 

쉐이딩 텀

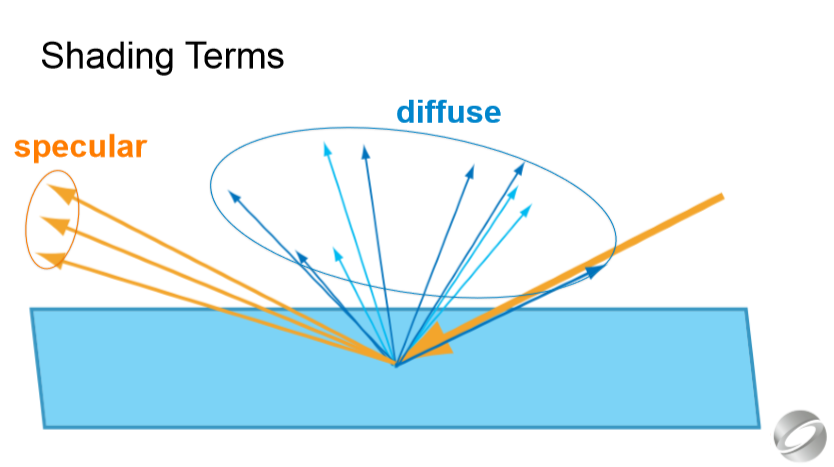
이 두 가지의 매우 다른 빛-물질 상호 작용 (표면 반사 및 굴절 흡수 - 산란)을 서로 다른 쉐이딩 텀(친숙한 "반사 specular"및 "확산 Diffuse")으로 나누면 편리합니다.

It is convenient to split these two very different light-material interactions (surface reflection and refraction-absorption-scattering) into different shading terms - the familiar “specular” and “diffuse”.

 

 

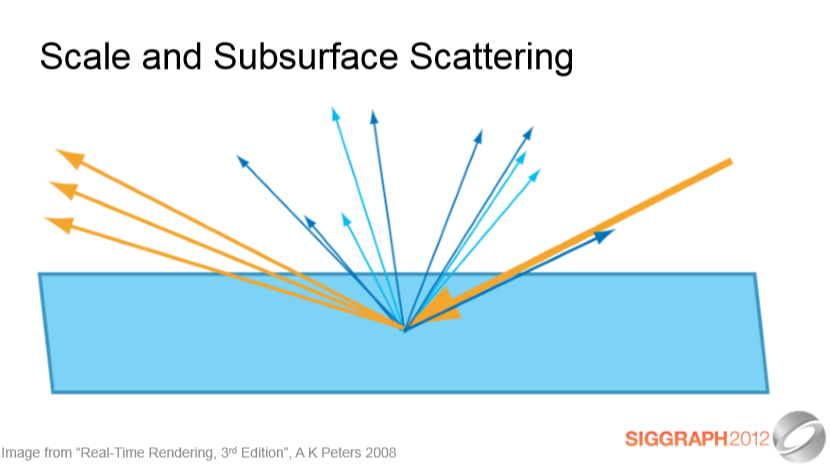
픽셀이 출입구(Entry-to-exit) 거리에 비해 작으면 (빨간색 원) 거리를 무시할 수 없으므로 특수한 렌더링 기술이 필요합니다. 이것들은 "표면하 산란 (suburface scattering)"이라고 불리지만 확산은 항상 표면하 산란 (subsurface scattering)이며, 그 차이는 스케일입니다. 

멀리 떨어진 피부나 대리석은 정상적인 렌더링 기술을 사용할 수 있으며 극단적인 클로즈업의 플라스틱은 "표면하 산란"기술을 필요로 합니다.

If the pixel is small (red circle) compared to the entry-exit distances, you can’t ignore the distances and need specialized rendering techniques. These are referred to as “subsurface scattering”, but diffuse is always subsurface scattering - the difference is the scale. So distant skin or marble can use normal rendering techniques, and plastic in extreme close up would need “subsurface scattering” techniques

 

 

물리적인 음영의 수학 - 빛의 물리학을 수학적 모델로 바꾸기 위한 첫 번째 단계는 빛을 숫자로 정량화하는 것입니다.

Math of physical shading - to turn light physics into a mathematical model, the first step is to quantify light as a number.

 

 

Radiometry는 빛의 측정입니다. 다양한 방사량 중 하나의 광선을 따라 빛의 강도를 측정하는 광도를 사용합니다. 래디언스는 스펙트럼 (파장에 따라 다양함)입니다. 기술적으로 연속적인 스펙트럼 배율 분포이지만 생산을 위해서는 RGB 값으로 표시됩니다.

Radiometry is the measurement of light. Of the various radiometric quantities, we’ll use radiance, which measures the intensity of light along a single ray. Radiance is spectral (varies with wavelength) - it’s technically a continuous spectral power distribution but for production purposes it’s represented as an RGB value.

 

 

로컬 셰이딩

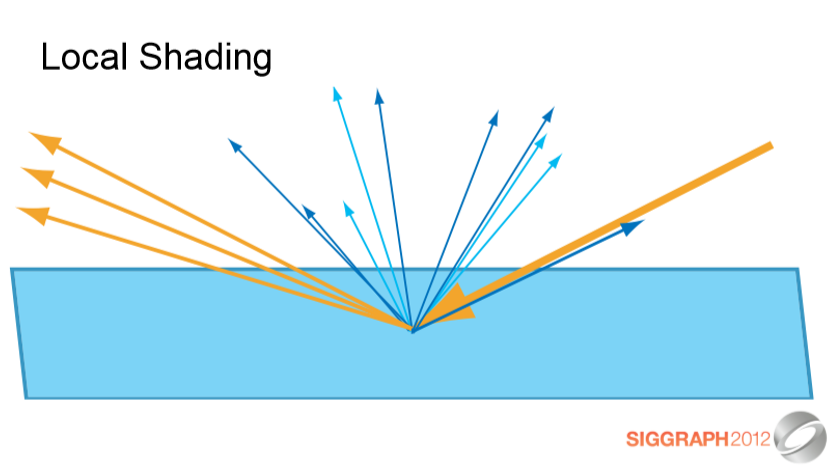
음영이 국부적으로 처리될 수 있다고 가정하면, 표면 지점에서의 빛 반응은 빛과 방향을 보고 있는 것에만 의존합니다.

 

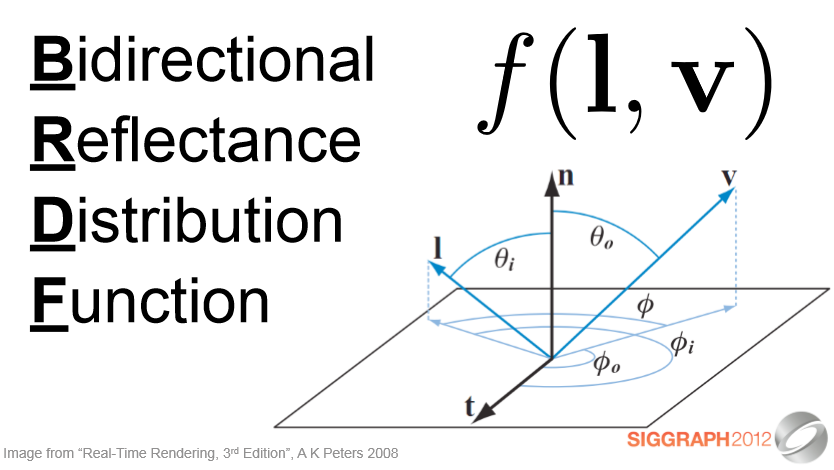
BRDF(Bidirectional Reflectance Distribution Function)

• 양방향의
• 반사율
• 분포
• 함수

 

우리는이 변화를 빛과 시야 방향의 함수인 BRDF(Bidirectional Reflectance Distribution Function)로 나타냅니다.

원칙적으로 BRDF는 4D 또는 3D 기능입니다.

실제로는 다양한 각도의 각도가 계산에 사용됩니다. 

BRDF는 거시적인 표면 위의 빛 및 뷰 벡터에 대해서만 정의됩니다. 역광 방향은 피해야 하며, 최소한 기여도에 0을 곱해야 합니다.
백페이싱 서페이스에 대해서는 뷰 방향을 뒤집는 것이 이론적으로 불가능하지만 보간 된 법선 또는 노멀 매핑을 사용하여 발생할 수 있습니다. 이들은 일반적으로 n-dot-v 곱을 0으로 클램핑 하거나 음수 값을 피하기 위해 절대 값을 취함으로써 처리됩니다.

We represent this variation with the BRDF, a function of light and view direction. In principle, the BRDF is a 4D or 3D function. 
In practice, a varying number of angles are used to compute it. The BRDF is only defined for light and view vectors above the macroscopic surface. Backfacing light directions should be avoided or at least have their contribution multiplied by 0. Backfacing view directions are theoretically impossible for opaque surfaces but may occur with interpolated normals or normal mapping; these are typically handled either by clamping the n-dot-v product to 0 or taking its absolute value to avoid negative values.

 

반사율 식

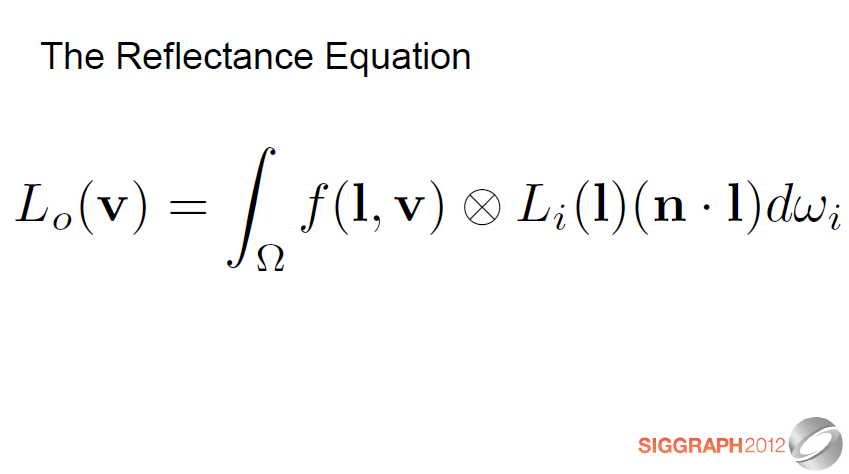
나가는 광도는 적분과 같습니다. (표면 위의 모든 방향에 대해) 들어오는 복사 시간 BRDF와 코사인 계수; "X in circle"은 구성 요소 별 벡터 (RGB) 곱셈을 나타냅니다.

Outgoing radiance equals the integral (over all directions above the surface) of incoming radiance times BRDF and cosine factor; “X in circle” denotes component-wise vector (RGB) multiplication.

 

표면 반사(스펙큘러 텀)

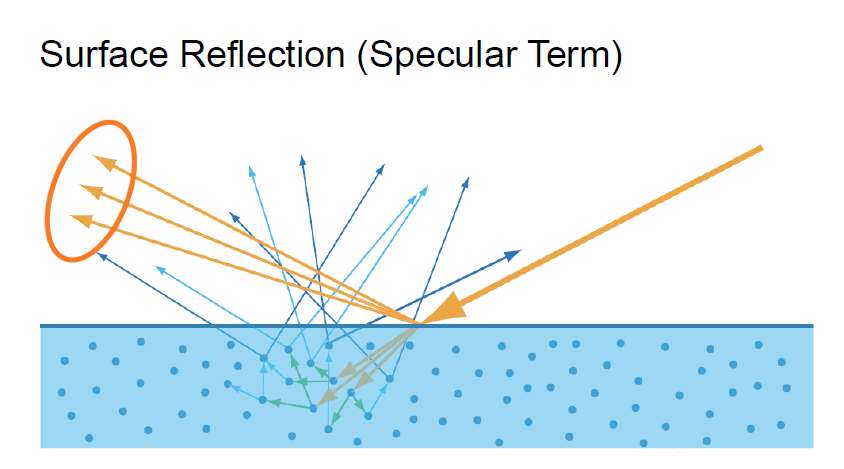
우리는 스펙큘러 텀을 먼저 보면서 시작해보죠.

We’ll start by looking at the specular term.

 

미세면 이론

미세면 이론(Microfacet theory)은 일반 (비 광학적으로 평평한) 표면에서 표면 (거울) 반사를 위해 BRDF를 유도하는 방법입니다.
그것은 표면이 많은 미세면으로 구성되어 있다고 가정합니다. 각 면은 완벽한 거울 (광학적으로 평평한 거울)이기 때문에 들어오는 각 광선을 한 방향으로만 반사시킵니다. 이 방향은 빛의 방향 l과 미세한 평면의 법선 m에 따라 달라집니다.

Microfacet theory is a way to derive BRDFs for surface (specular) reflection from general (non-optically flat) surfaces. 
It assumes the surface is composed of many microfacets. Each facet is a perfect mirror (optically flat), so it reflects each incoming ray of light into only one outgoing direction, which depends on the light direction l and the microfacet normal m.

 

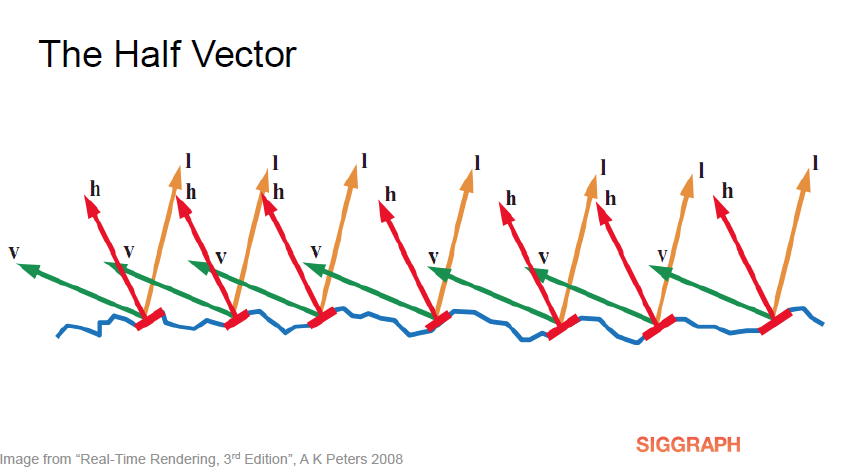
l과 v 사이의 정확히 중간에 배향된 표면 법선 m을 갖는 면만이 가시광선을 반사합니다.

이 방향은 하프 벡터 h입니다.

Only those microfacets which happen to have their surface normal m oriented exactly halfway between l and v will reflect any visible light - this direction is the half-vector h.

 

그림자 그리고 마스킹

m = h 인 모든 미세면들이 기여하는 것은 아닙니다. 일부는 l (섀도잉) 또는 v (마스킹)에서 다른 미세면으로 차단됩니다.

Not all microfacets with m = h will contribute - some will be blocked by other microfacets from either l (shadowing) or v (masking).

 

 

다중 표면 반사

실제로, 차단된 빛은 계속 튀어 오릅니다. 일부는 결국 BRDF에 기여할 것입니다. Microfacet BRDF는 이것을 무시하고 차단 된 모든 빛이 손실되었다고 가정합니다.

In reality, blocked light continues to bounce; some will eventually contribute to the BRDF. Microfacet BRDFs ignore this, and assume all blocked light is lost

 

미세면 이론

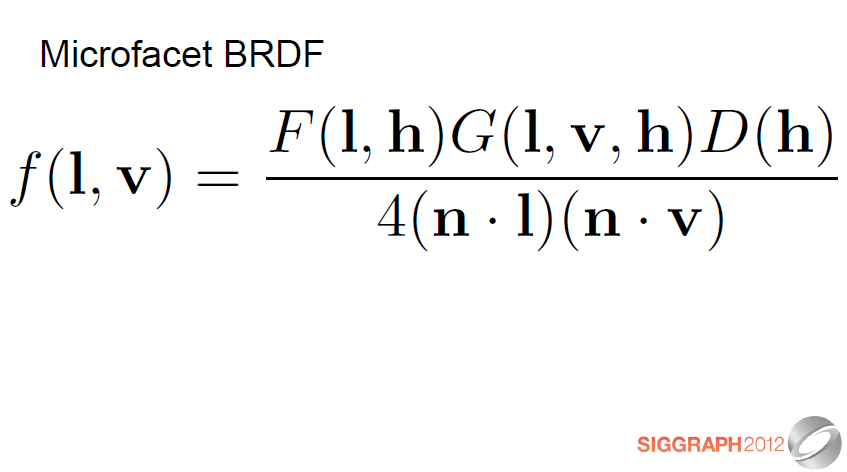
이것은 미세면 (microfacet) BRDF입니다. 각 부분을 설명하면서 다양한 부분을 살펴보겠습니다.

This is the microfacet BRDF. I’ll go over its various parts, explaining each.

 

 

프레넬 반사프

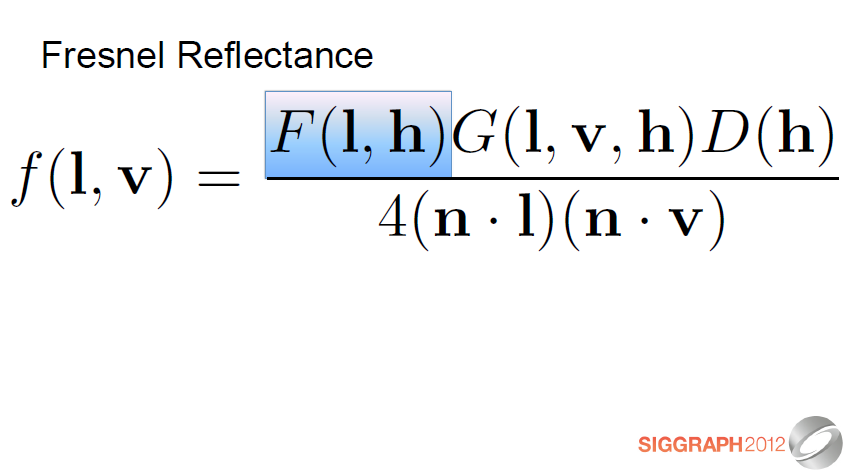
프레넬 반사율은 빛 방향과 표면 법선이 주어진 주어진 물질의 광학적으로 평평한 표면에서 반사된 (vs. 굴절된) 빛의 비율입니다. 이것은 우리에게 얼마나 많은 빛이 관련된 미세면에(반각 방향) 반사되는지를 알려줍니다.

The Fresnel reflectance is the fraction of incoming light reflected (vs. refracted) from an optically flat surface of a given substance given light direction and surface normal. This tells us much how much of the light hitting the relevant microfacets (the ones facing in
the half-angle direction) is reflected.

 

프레넬 반사율

프레넬 반사율은 굴절률 (즉, 물체가 만든 것)과 광각에 따라 달라집니다. 

이 그래프에서 3개의 라인을 가진 물질은 R, G 그리고 B, 한 라인은 무색의 반사율을 가지고 있습니다.

Fresnel reflectance depends on refraction index (in other words, what the object’s made of) and light angle. In this graph, substances with three lines are R, G and B – substances with one line have uncolored reflectance.

 

 

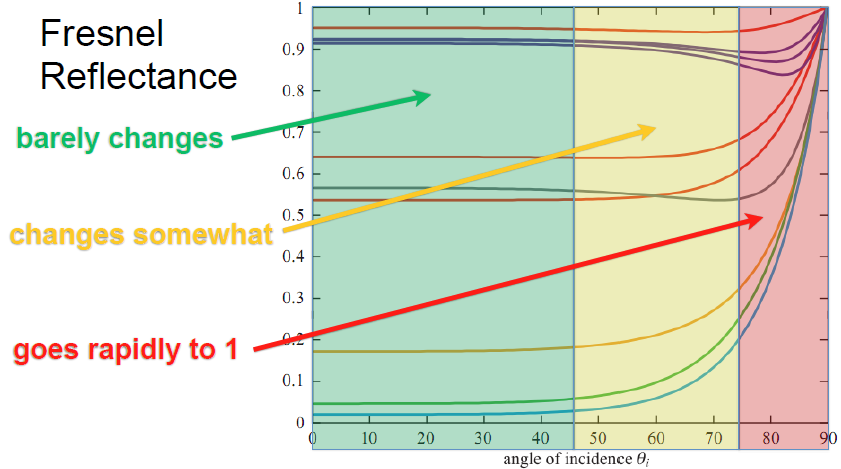
간신히 바뀌는 단계 / 뭔가 바뀌는 단계 / 가파르게 1로 바뀌는 단계

 

각도가 증가함에 따라, 처음에는 프레넬 반사율은 거의 동일하게 유지되고, 

매우 반짝이는 각도의 경우 모든 파장에서 100 %로 이동합니다.

As angle increases, at first the Fresnel reflectance stays almost the same, then for very glancing angles it goes to 100% at all wavelengths.

 

 

표면 특유의 반사 색상인가? : C_spec

 

대부분의 각도에 대한 반사율은 수직 입사각에 가깝기 때문에 법선 입사 반사율 F(0)은 표면의 고유한 반사 색상입니다.

Since the reflectance over most angles is close to that at normal incidence, the normal-incidence reflectance F(0) is the surface’s characteristic specular color.

 

 

금속에 대한 수직 입사(F(0)) 프레넬

 

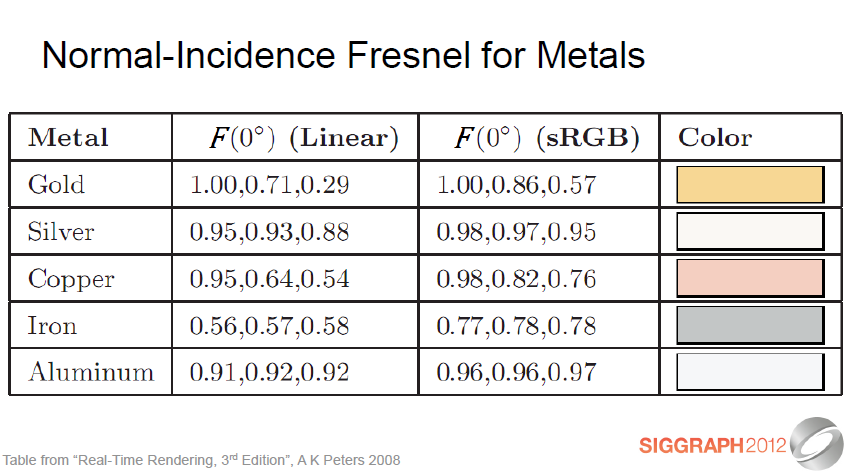
금속에는 표면하 텀(subsurface term)이 없으므로 표면의 프레넬 반사율은 재료의 유일한 색상원입니다. 

"선형"및 "sRGB"열은 값이 선형 또는 감마 공간에 있는지 여부를 나타냅니다. 금속의 경우 반사 색상이 모두 상대적으로 높습니다.

Note that metals have no subsurface term, so the surface Fresnel reflectance is the material’s only source of color. The “linear” and “sRGB” columns refer to whether the values are in linear or gamma space. Note that for metals the specular colors are all relatively high.

 

 

비금속에 대한 수직 입사(F(0)) 프레넬

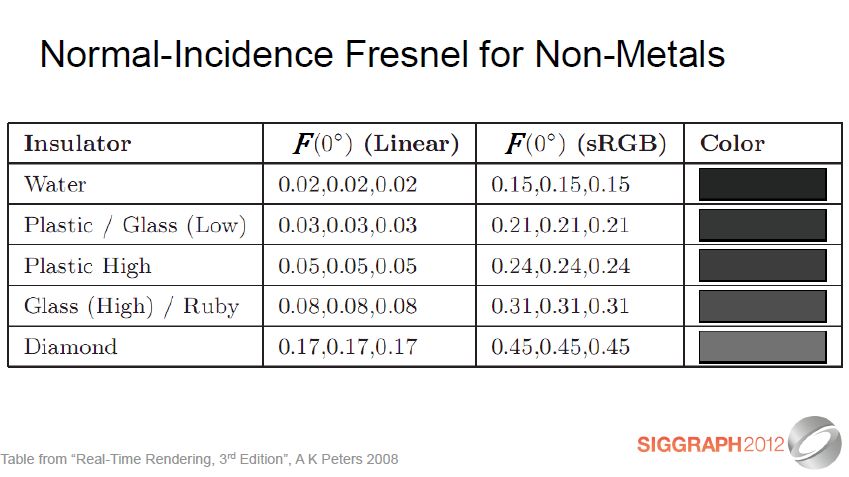
대부분의 비금속에는 이 프레넬 (반사) 반사율 외에도 표면하(확산) 색상이 있습니다. 

비금속의 경우 반사 색상은 무채색 (회색)이며 상대적으로 낮습니다 (특히 보석과 결정을 제외하면).

Most non-metals also have a subsurface (diffuse) color in addition to this Fresnel (specular) reflectance. Note that for non-metals the specular colors are achromatic (gray) and are relatively low (especially if excluding gems and crystals).

 

 

프레넬에 대한 Schlick 근사법

꽤 정확한, 값싼, C_spec의 파라미터화가 가능한 

 

Fresnel 표현에는 일반적으로 Schlick 근사가 사용됩니다. 그것은 싸고 합리적으로 정확합니다 - 더 중요한 것은 편리한 매개 변수 (수직 입사 프레넬 반사율 또는 반사 색상)를 가집니다.

The Schlick approximation to Fresnel is commonly used. It is cheap and reasonably accurate - more importantly it has a convenient parameter (normal incidence Fresnel reflectance, or specular color).

 

미세면 노말 분포

미세면 노말 분포는 주어진 방향 (이 경우, 반각 방향)을 가리키는 미세면 법선의 농도가 무엇인지 알려줍니다. NDF는 하이라이트의 크기와 모양을 결정합니다.

The microfacet normal distribution tells us what is the concentration of microfacet normals pointing in a given direction (in this case, the half-angle direction). The NDF determines the size and shape of the highlight.

 

 

기하학 인자

 

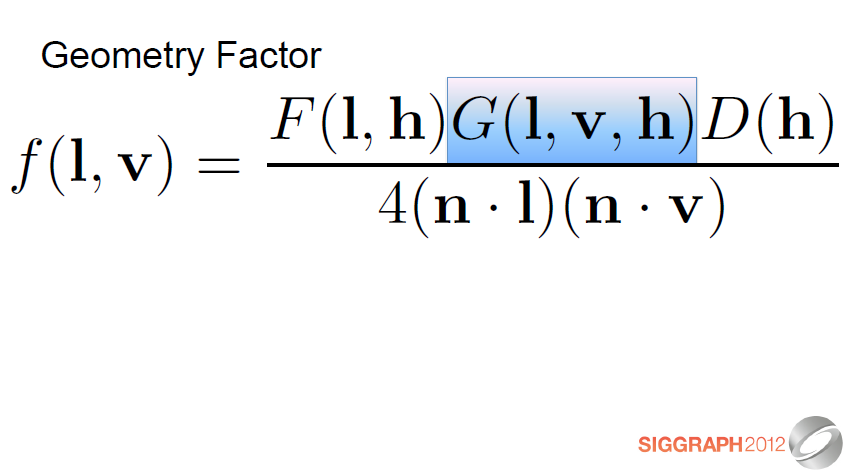
기하학 인자는 주어진 방향의 미세면이 주어진 l 및 v 방향으로부터 조명되고 가시화 (예를 들어, 음영 및 / 또는 마스크 되지 않음) 될 기회를 제공한다.

The geometry factor gives the chance that a microfacet of the given orientation is lit and visible (e.g., not shadowed and/or masked) from the given l and v directions.

 

 

표면하 반사 (확산 반사 텀)

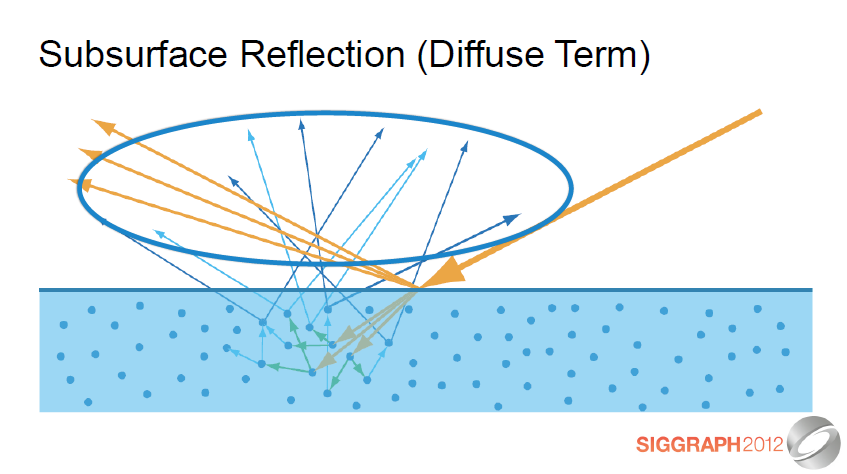
다음으로, 우리는 확산(Diffuse) 또는 표면하(subsurface) 텀을 간략하게 살펴볼 것입니다.

Next, we’ll take a quick look at the diffuse or subsurface term.

 

램버트(=람베르트)

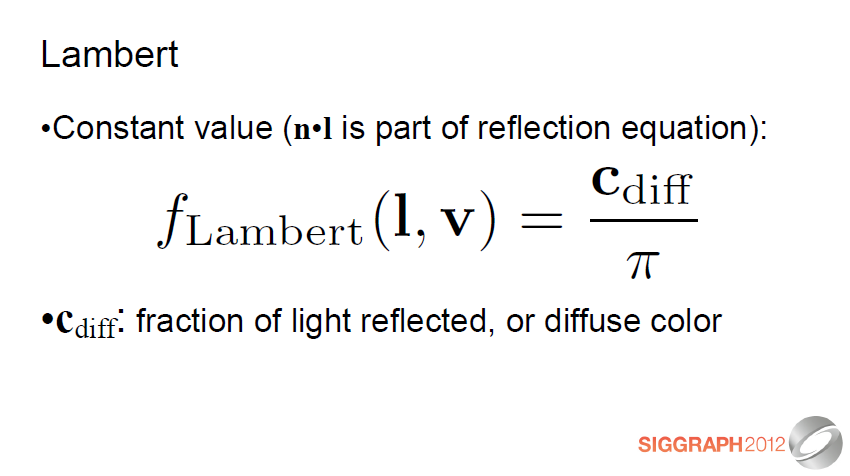
• 상수값(n·l은 반사 방정식의 일부입니다)
• C_diff: 반사된 빛의 일부 또는 확산 색

램버트 모델은 게임 및 영화 제작에 사용되는 가장 보편적인 확산 용어입니다. 그 자체로 가능한 가장 단순한 BRDF입니다. 상수값 (잘 알려진 코사인 인수는 반사 방정식의 일부입니다).

 

 

확산 반사와 표면 반사의 교환

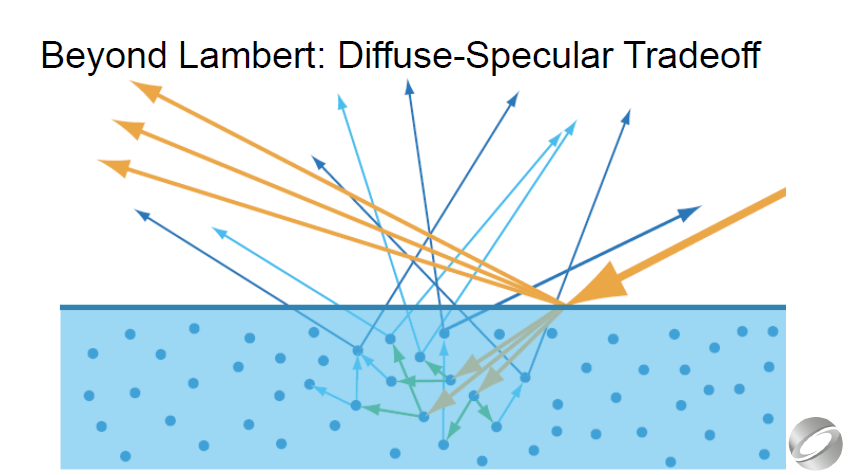
램버트가 설명하지 않는 몇 가지 중요한 물리적 현상이 있습니다. 확산은 굴절된 빛에서 비롯됩니다.
어떤 의미에서 스펙큘러(specular, 표면 반사) 텀은 들어오는 빛에 "찜"한 것을 가져오고 디퓨즈(diffuse, 확산 반사)는 나머지를 얻습니다.

표면 반사는 시선각으로 100 %가 되기 때문에 확산은 0 %가 되어야 합니다. 이것을 설명하는 다양한 방법이 있습니다. 아마도 가장 간단한 방법은 확산을 곱하는 것입니다. (1-F) (이것은 Fresnel을 반사와 확산 사이의 "lerp factor"로 바꿉니다).

There are a few important physicaly phenomena that Lambert doesn’t account for. Diffuse comes from refracted light - in a sense the
specular term gets “dibs” on the incoming light and diffuse gets the leftovers. Since surface reflection goes to 100% at glancing
angles, it follows that diffuse should go to 0%. There are various ways to account for this - perhaps the simplest is to multiply diffuse
by (1-F) (this turns Fresnel into a “lerp factor” between specular and diffuse).

 

 

표면 거칠기

램버트가 모델링하지 않은 또 다른 현상은 표면 거칠기의 영향입니다.

거칠기는 일반적으로 반사에만 영향을 줍니다. 점에서의 확산 반사율은 영역을 가로질러 오는 입사광으로부터 오는 것이기 때문에, 미세 기하학적 변화는 확산 반사율에 대해 평균화되는 경향이 있습니다.

그러나 일부 표면은 산란 거리보다 큰 미세 기하학을 가지고 있으며 확산에 영향을 미칩니다. 이것들은 Oren-Nayar 나 Minneart와 같은 특수화된 확산 모델로 모델링 되어야 하는 표면입니다.

Another phenomenon not modeled by Lambert is the effect of surface roughness. Roughness typically only affects specular; since diffuse reflectance at a point comes from incoming light over an area, the microgeometry variations tend to be averaged out for diffuse reflectance. But some surfaces have microgeometry larger than the scattering distance, and these do affect diffuse. These are the surfaces that should be modeled with specialized diffuse models like Oren-Nayar or Minneart.

 

 

물리적 셰이딩 모델 구현하기

• 렌더러에 쉐이딩 방정식을 구현하려면 다양한 조명 모델과 결합하세요.
  
  • 일반 조명
  • 이미지 베이스드 조명
  • 공간 광원
  • 점등 광원
  • 환경광

일반 조명 : BRDF를 모든 방향 (지역 광원, 스카이라이트, 간접 반사)에서 지속적으로 들어오는 빛과 통합합니다. - 광선 추적과 같은 GI 알고리즘이 필요합니다. 

이미지 기반 조명은 환경 맵 등을 의미합니다. 에어리어 광원은 영화에서는 일반적으로 사용되기 시작하지만 게임에서는 그렇지 않습니다. 일반적으로 점등 광원을 사용합니다 (필름에서도 여전히 사용됨). 

Ambient는 가장 단순한 조명 모델입니다. 모든 방향의 일정한 조명입니다. 우리는 게임 및 영화 제작 렌더링에서 공통적으로 사용되기 때문에 지키는 조명과 이미지 기반 조명에 대해 더 자세히 이야기할 것입니다.

General lighting: integrate BRDF against continuous incoming light from all directions (area light sources, skylight, indirect reflections) - requires GI algorithm like ray-tracing. Image-based lighting refers to environment maps and the like. Area light sources are starting to be commonly used in film but not in games, which typically use punctual light sources (still used in film as  well). Ambient is the simplest lighting model - just constant light from all directions. We will talk more about punctual lights and image-based lighting due to their common use in game and film production rendering

 

점등 광원

• 빛의 색 c_light 그리고 라이트 위치에서의 방향 l_c 을 파라미터화 할 수 있음
• c_light 90 도의 빛에 의해 조명된 흰색 램버트식 표면의 밝기와 같습니다.

이들은 게임과 영화에서 일반적으로 사용됩니다 - 아주 작고 매우 밝아서 현실적이지는 않지만 임의의 BRDF로 구현할 수 있는 가장 쉬운 유형의 빛입니다. 표면이 거친면에서는 괜찮아 보이고 매끄러운 면에서는 그렇지 않습니다. 

점등 광원은 색상과 방향에 따라 파라미터화 됩니다.

These are commonly used in games and film - infinitely small and infinitely bright, they are not realistic, but are the easiest type of light to implement with arbitrary BRDFs. They look OK for rough surfaces, not so much for smooth ones. Punctual lights are parameterized by color and direction

 

점등 광원 반사 방정식

코스 노트에 방정식 유도가 있습니다. 

게임은 백페이싱(backfacing) 광원을 건너뛰는 편리한 방법으로 내적을 클램프 시키는 경우가 있습니다.

The course notes have the derivation. Games often clamp the dot product as a convenient method of skipping backfacing lights

 

이미지 베이스드 라이팅

• 완벽하게 매끄러운 표면은 쉽습니다 - 단지 프레넬 함수에 곱하면 됩니다.
  C_spec 같이, 다른 각도는 :
  • F(l,h) 대신으로서 F(v,n) (또는 F(v,h)와 같음) 
• 정확한 광택/확산에는 많은 샘플이 필요합니다.
  • Importance sampling의 도움
  • 미리 필터링하기 (단독 또는 Importance sampling과 같이)

이미지 기반 조명은 모든 재질에 유용하지만 특히 매끄럽거나 금속성 재질에 유용합니다. 

게임은 사전 필터링을 많이 사용합니다. - Importance Sampling을 사용하는 경향이 있습니다 (사전 필터링과 결합되는 경우도 있음).

Image-based lighting is useful for all materials, but especially for smooth or metallic ones. 

Games use prefiltering heavily - film tends to use importance sampling (sometimes combined with prefiltering).

 

Building a Microfacet Model

미세면 모델 구축

• D()와 G()의 선택은 독립적입니다. 당신은 다른 모델들과 믹스 앤 매치할 수 있습니다.
• 새로운 BRDF 모델을 제안하는 대부분의 논문은 실제로 새로운 D() 또는 새로운 G()입니다.

이제 우리는 미세면 모델을 구축하기 위한 몇 가지 옵션을 살펴볼 것입니다. 

방정식을 복사하는 것에 대해 걱정하지 마십시오. 모두 코스 노트에 있습니다.

We will now look at some options for building a microfacet model. Don’t worry about copying the equations down - they will all be in the course notes

 

microfacet BRDF에서 사용하려면, 위의 방정식에 따라 NDF를 정규화해야 합니다. 

정규화되지 않은 텀이 있는 경우 코사인 가중치로 나눕니다. 

일반적인 경우, 적분은 구 위에 있지만 반구에 통합하려는 높이 필드 서페이스만 처리합니다. 

Heightfield NDF는 역(backfacing) 방향에 대해 항상 0으로 평가되어야 합니다. 

이러한 방향에 대해 평가할 수 있다면 (예 : 보통 매핑으로 인해 하프 벡터가 뒤틀리는 경우가 있음) 이러한 경우 0으로 평가해야 합니다. 

90도에서 0이 되는 NDF의 경우, 이는 n-dot-m 내적을 0으로 클램핑함으로써 간단히 수행할 수 있습니다. 

다른 NDF는 조건식을 요구할 수 있습니다.

To be used in a microfacet BRDF, an NDF should be normalized based on the equation above. If you have a non-normalized term, just divide it by its cosine-weighted integral. In the general case the integral is over the sphere but we will only deal with heightfield surfaces where you want to integrate over the hemisphere. Heightfield NDFs should always evaluate to 0 for backfacing directions; if you may evaluate it for these directions (e.g. normal mapping can sometimes cause backfacing half-vectors) then you should ensure it evaluates to 0 in these cases. For NDFs that go to 0 at 90 degrees this can simply be done by clamping the n-dot-m dot product to 0; other NDFs may require a conditional expression.

 

 

올바르게 정규화된 Phong (cosine power lobe)은 유효한 NDF가 됩니다.

Correctly normalized, the Phong (cosine power lobe) becomes a valid NDF.

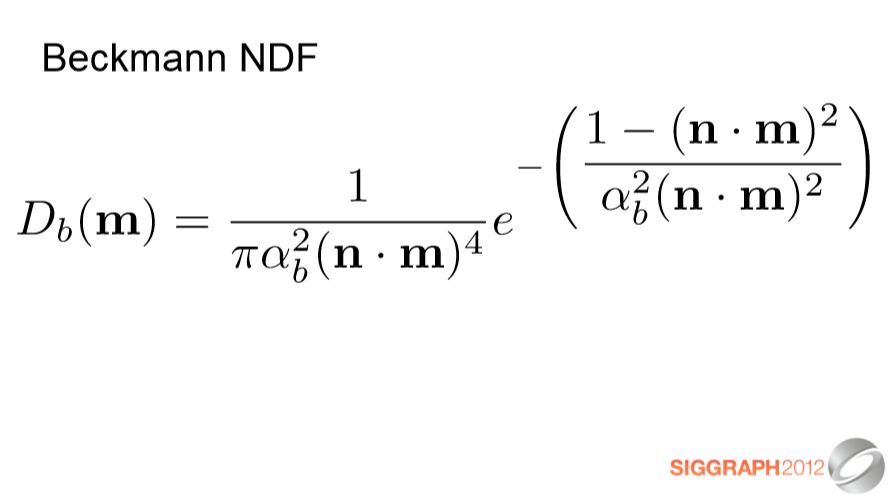
Beckmann NDF는 Phong과 몇 가지 중요한 점에서 유사하며 다른 점도 다릅니다. 

자세한 내용은 코스 노트를 참조하세요.

The Beckmann NDF is similar to Phong in some important ways and different in others - see the course notes for more details.

 

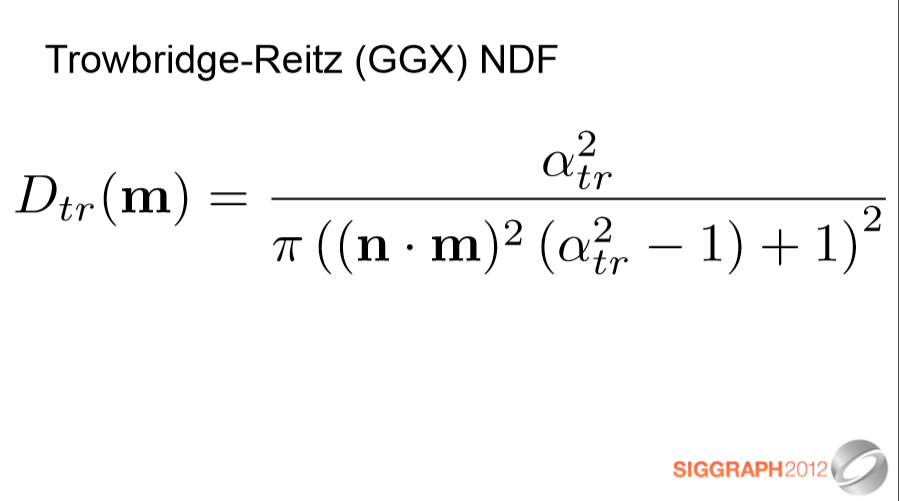
Trowbridge-Reitz NDF는 Phong & Beckmann과는 근본적으로 다른 모양을 가지고 있는데, 

좁은 "피크"와 더 넓은 "꼬리"가 있습니다. 자세한 내용은 코스 노트에서 확인할 수 있습니다.

The Trowbridge-Reitz NDF has a fundamentally different shape than Phong & Beckmann, 

with a narrower “peak” and broader “tails”. More details can be found in the course notes.

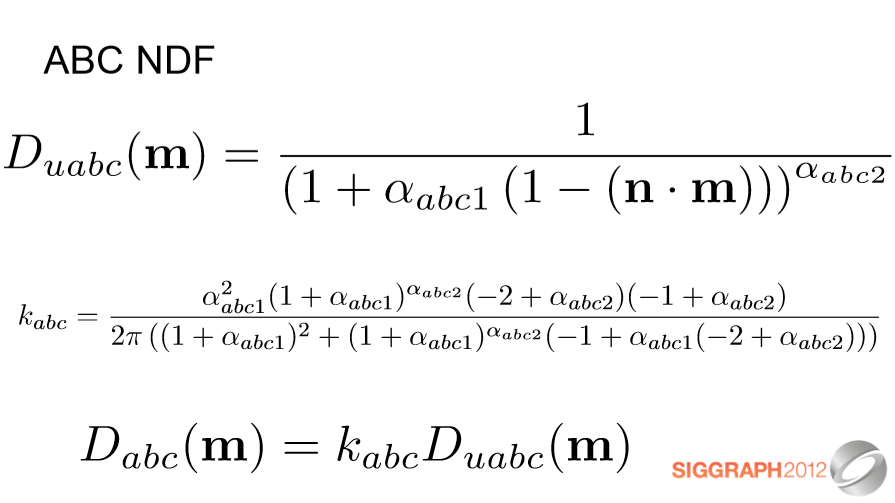
ABC 기능은 NDF가 아닌 표면 고지대의 분광 분포와 같이 광학 공학 공동체에서 잠시 동안 사용되어 왔습니다. 최근 연구에서는 이 기능을 NDF로 사용하도록 제안했습니다. 저는 Mathematica에서 정규화 인수를 얻었으며 이를 단순화하거나 최적화하는 데 시간을 낭비하지 않았습니다. αabc2 = 1.0 및 αabc2 = 2.0에서 특이점을 갖는다는 점에 유의하십시오. 나는 훨씬 더 싼 커브가 그것에 맞을 수 있다고 생각한다. 자세한 내용은 코스 노트에서 확인할 수 있습니다.

The ABC function has been around for a while in the optical engineering community, not as an NDF but as a spectral power distribution for the heightfield of the surface. Recent work has proposed using this function as an NDF. I got the normalization factor from Mathematica and didn’t spend any time simplifying or optimizing it; note that it has singularities at αabc2=1.0 and αabc2=2.0. I suspect a much cheaper curve could be fit to it. More details can be found in the course notes.

쉬프트 - 감마 NDF는 비교적 새로운 것입니다. ABC와 마찬가지로 대부분의 등방성 NDF에는 단일 조도 매개 변수가 아니라 두 개의 매개 변수가 있습니다. ABC와 마찬가지로 정규화 계수는 비싸지만 값싼 근삿값을 찾을 수 있습니다. 다시 ABC와 마찬가지로이 NDF를 제안한 저자는 이전 모델보다 측정된 BRDF (예 : Matusik 데이터베이스)에 더 가깝다고 제안합니다

The shifted-Gamma NDF is a relatively new one. 

Like ABC it has two parameters, rather than the single roughness parameter most isotropic NDFs have. Like ABC, its normalization factor looks expensive, but a cheap approximation could likely be found. Again similarly to ABC, the authors who proposed this NDF suggest that it is a closer fit to measured BRDFs (such as the Matusik database) than previous models

경우에 따라, 기하학 인자를 n dot-l-times-n-dot-v "단축 텀"으로 나눈 표현식이 있습니다. 

이 결합된 용어를 "가시성 텀"라고 부를 것입니다. 

다음 슬라이드는 지오메트리 요소 또는 전체 가시성 텀을 나타내는 몇 가지 선택 사항을 설명합니다.

In some cases, expressions are found for the geometry factor divided by the n-dot-l-times-n-dot-v “foreshortening term”. We’ll call this combined term the “visibility term”. The following slides will describe some choices for representing either just the geometry factor or the entire visibility term

 

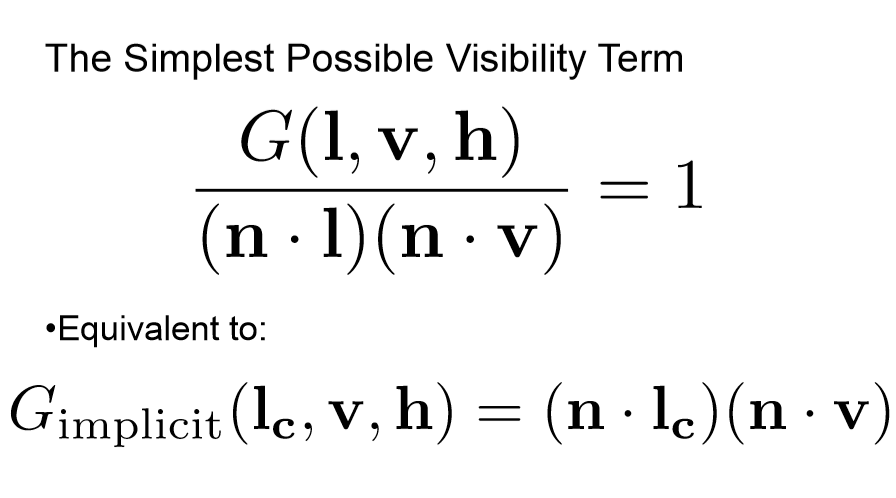
많은 BRDF (특히 게임)에는 가시성 텀이 전혀 없습니다. 

이는 가시성 텀이 1과 동일하다는 것을 의미합니다. 이는 n-dot-l-times-n-dot-v와 동일한 기하학적 요소를 의미합니다. 

이 "함축적"기하학적 요소는 그럴듯합니다. 보기와 빛이 법선 방향 일 때 하나는 같고 둘 중 하나가 90 도일 때 0입니다. 전체 가시성 텀이 없기 때문에 "공짜"보다 저렴합니다. 

그러나 glancing angle (실제 물질에 비해)이 너무 빠르며 거칠기의 영향을 받지 않습니다.

Many BRDFs (especially game ones) have no visibility term at all. This means the visibility term is effectively equal to one, which implies a geometry factor equal to n-dot-l-times-n-dot-v. This “implicit” geometry factor is plausible - it equals one when view and light are in the normal direction, and zero when either one of them is at 90 degrees. And it is “cheaper than free” since the entire visibility term is missing. But it goes to 0 too fast at glancing angles (compared to real-world materials) and it isn’t affected by roughness, which is implausible

 

이것은 실제로 Torrance-Sparrow 기하학 요소의 재구성으로서 Blinn에 의해 1975 년에 발명되었습니다. 수년 동안 (특히 필름에서) 많이 사용되었지만 비현실적인 미세 기하학 모델 (긴 홈으로 구성되는 등방성 표면)을 기반으로 하며 거칠기의 영향을 받지는 못합니다.

This was actually invented by Blinn in 1975 as a reformulation of the Torrance-Sparrow geometry factor. 

It’s been used a lot over the years (especially in film), but it has some problems: it’s based on an unrealistic microgeometry model (isotropic surface composed of infinity long grooves) and it’s not affected by roughness, which is implausible.

 

다른 문제 외에도 Cook-Torrance는 게임에서 쓰기엔 비용이 비싼 편입니다. 그러나 그것에 대한 매우 저렴하고 효과적인 근사치가 있습니다. 함축적인 기하학 팩터만큼 저렴합니다 - 프레넬 (Fresnel)을 계산할 필요가 있는 내적(dot product)의 제곱으로 나누면 됩니다.

In addition to its other issues, Cook-Torrance is a little on the expensive side for games. 

There is a very cheap and effective approximation for it however; 

almost as cheap as the implicit geometry factor - you just need to divide by the square of a dot product that you need to compute anyway for Fresnel

 

 

이것은 아마도 오늘 사용하는 것이 가장 좋습니다. 이것은 거칠기의 영향을 받으며 모든 NDF에 대해 일치하는 기하학적 요소를 생성하는 프로세스로 일반화되었습니다. NDF를 연결하고 일치하는 기하학 요소를 얻는 "블랙박스"라고 생각할 수 있습니다. 이 프로세스는 분석 표현을 초래하지 않을 수도 있지만, 어떤 경우에도 결과에 더 간단한 곡선을 나타낼 가능성이 가장 높기 때문에 이 방법이 유용합니다. 이 함수에 대한 Schlick 근사치 (내 자신의 책을 포함하여 많은 곳에서 참조되었습니다)은 잘못된 버전의 Smith와 비슷하므로 정확하지 않습니다. 스미스 음영 요소에 대한 자세한 내용은 코스 노트에서 확인할 수 있습니다.

This is probably the best one to use today. It is affected by the roughness, and it has been generalized to a process for generating a matching geometry factor for any NDF. You can think of it as a “black box” where you plug in an NDF and get a matching geometry factor. The process may not result in an analytical expression but that’s fine since you most likely want to fit a simpler curve to the result in any case. Note that the Schlick approximation to this function (which has been referenced in many places - including my own book!) is not correct since it approximates the wrong version of Smith. More details on the Smith shadowing factor can be found in the course notes.